Question

N

2) A sample of size n= 49 is obtained. The population mean

is m= 80 and the population standard deviation is s = 14.

Find the probability that the sample has a sample average

between 78.3 and 85.1, (5 points)

-

Answer 1

P(78.3 < x' < 85.1) = 0.7969

Explanation:

Given:

Sample size, n = 49

mean, u = 80

Standard deviation
`\sigma` = 14

Sample mean, ux' = population mean = 80

Let's find the sample standard deviation using the formula:

`\sigma \bar x = (\sigma)/(√(n))`

`= (14)/(√(49)) = (14)/(7) = 2`

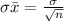
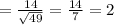
To find the probability that the sample has a sample average between 78.3 and 85.1, we have:

`P(78.3 < \bar x < 85.1) = (P[(78.3 -80))/(2) < ((\bar x - u \bar x))/(\sigma \bar x) < ((85.1 -80))/(2)]`

= P( -0.85 < Z < 2.55 )

= P(Z < 2.55) - P(Z <-0.85 )

Using the standard normal table, we have:

= 0.9946 - 0.1977 = 0.7969

Approximately 0.80

Therefore, the probability that the sample has a sample average between 78.3 and 85.1 is 0.7969

Answer 2

0.7969

Explanation:

Given that: A sample of size n= 49 is obtained. The population mean is m= 80 and the population standard deviation is s = 14.

The z score measures the number of standard deviation by which the raw sore is above or below the mean. It is given by the equation:

`z=(x-m)/((s)/(√(n) ) )`

For x = 78.3, the z score is:

`z=(x-m)/((s)/(√(n) ) )=(78.3-80)/((14)/(√(49) ) ) =-0.85`

For x = 85.1, the z score is:

`z=(x-m)/((s)/(√(n) ) )=(85.1-80)/((14)/(√(49) ) ) =2.55`

P(78.3<x<85.1) = P(-0.85<z<2.55) = P(z<2.55) - P(z<-0.85) = 0.9946 - 0.1977 = 0.7969