Question

On a coordinate plane, a circle has a center at (0, 0). Point (3, 0) lies on the circle.

Distance formula: StartRoot (x 2 minus x 1) squared + (y 2 minus y 1) squared EndRoot


Does the point (2, StartRoot 6 EndRoot) lie on the circle shown? Explain.


Yes, the distance from (3, 0) to (0, 0) is 3 units.

Yes, the distance from (0, 0) to (2, StartRoot 6 EndRoot) is 3 units.

No, the distance from (3, 0) to (2, StartRoot 6 EndRoot) is not 3 units.

No, the distance from (0, 0) to (2, StartRoot 6 EndRoot) is not 3 units.

Answer 1

d

Explanation:

Answer 2

The correct option is;

No, the distance from (0, 0) to (2, √6) is not 3 units

Explanation:

The given parameters of the question are as follows;

Circle center (h, k) = (0, 0)

Point on the circle (x, y) = (3, 0)

We are required to verify whether point (2, √6) lie on the circle

We note that the radius of the circle is given by the equation of the circle as follows;

`Distance \, formula = \sqrt{\left (x_(2)-x_(1) \right )^(2) + \left (y_(2)-y_(1) \right )^(2)}`

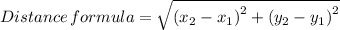
Distance² = (x - h)² + (y - k)² = r² which gives;

(3 - 0)² + (0 - 0)² = 3²

Hence r² = 3² and r = 3 units

We check the distance of the point (2, √6) from the center of the circle (0, 0) as follows;

`\sqrt{\left (x_(2)-x_(1) \right )^(2) + \left (y_(2)-y_(1) \right )^(2)} = Distance`

Therefore;

(2 - 0)² + (√6 - 0)² = 2² + √6² = 4 + 6 = 10 = √10²

`\sqrt{\left (2-0 \right )^(2) + \left (√(6) -0 \right )^(2)} = 10`

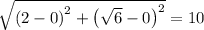
Which gives the distance of the point (2, √6) from the center of the circle (0, 0) = √10

Hence the distance from the circle center (0, 0) to (2, √6) is not √10 which s more than 3 units hence the point (2, √6), does not lie on the circle.