Question

Points E, F, and D are located on circle C. Circle C is shown. Line segments E C and D F are radii. Lines are drawn from points E and D to point F to form chords E F and D F. Arc E D is 68 degrees. The measure of arc ED is 68°. What is the measure of angle EFD? 34° 68° 112° 132°

Answer 1

34 (100% Correct)

Explanation:

Answer 2

Option (1). 34°

Explanation:

From the figure attached, CE and CD are the radii of the circle C.

Central angle CED formed by the intercepted arc DE = 68°

Since measure of an arc = central angle formed by the intercepted arc

Therefore, m∠CED = 68°

Since m∠EFD =
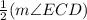`(1)/(2)(m\angle ECD)` [Central angle of an intercepted arc measure the double of the inscribed angle by the same arc]

Therefore, m∠EFD =
`(1)/(2)(68)`

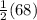
= 34°

Therefore, Option (1) 34° will be the answer.