Question

QUALITY CONTROL1)Specifications for a part for a DVD player state that the part should weigh between 24.6 and 25.6 ounces. The process that produces the parts has a mean of 25.1 ounces and a standard deviation of .26 ounce. The distribution of output is normal. a)What control chart will you use and why?b)With a 2-sigma confidence, what are the upper and lower control limitsif sample of n = 11are taken and the process is in control (random)?c)Is the process in control

Answer 1

Explanation:

Given that,

μ = 25.1

σ = 0.26

a) since standard deviation is ideal measure of dispersion , a combination of control chart for mean x and standard deviation known as

`\bar x \\\text {and}\\\mu`

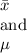
Chart is more appropriate than
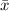`\bar x` and R - chart for controlling process average and variability

so we use

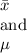`\bar x \\\text {and}\\\mu`charts

b)

n = 11

we have use 2 σ confidence

so, control unit for
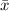`\bar x` chart are

upper control limit =
`\mu +2*( \sigma)/(√(n) )`

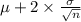
lower control limit =
`\mu -2*( \sigma)/(√(n) )`

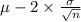
control limit = μ

μ = 25.1

upper control limit =

`25.1+2* (0.26)/(√(11) ) \\\\=25.2567`

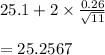
lower control limit =

`25.1-2* (0.26)/(√(11) ) \\\\=24.9432`

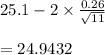
Upper control limit and lower control limit are in between the specification limits , that is in between 24.9 and 25.6

so, process is in control

c) if we use 3 sigma limit with n = 11

then

upper control limit =
`\mu +3*( \sigma)/(√(n) )`

`25.1+3*(0.26)/(√(11) ) \\\\=25.3351`

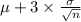
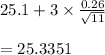
lower control limit =
`\mu -2*( \sigma)/(√(n) )`

`25.1-3*(0.26)/(√(11) ) \\\\=24.8648`

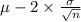
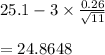
control limit is 25.1

Then, process is in control since upper control limit and lower control limit lies between specification limit

So, process is in control