Answer:
The required probability is
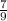 .
.
Explanation:
Set given is:
S = {1, 2, 3, 5, 15, 21, 29, 38, 500}
Total number of elements in set,
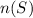 = 9
= 9
Let A be the event that the number is less than 29 ({1, 2, 3, 5, 15, 21}).
Number of items in the event A,
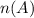 = 6
= 6
Probability of event A,
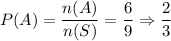
Formula for probability of any event E:
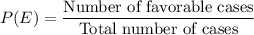
Let B be the event that the number is odd (either of {1,3,5,15,21,29}).
Number of items in the event B,
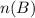 = 6
= 6
Probability of event B,
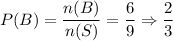
The event A and B have a few elements in common, i.e. numbers less than 29 which are odd as well.
The common elements are represented as:
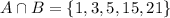
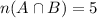
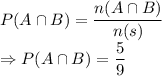
To find probability of selecting a number which is either less than 29 (event A) or odd (event B),
We have to find
 which is represented as
which is represented as
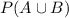 and the formula is:
and the formula is:
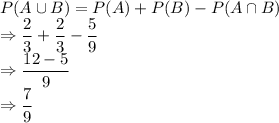
The required probability is
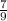 .
.