Answer:
$11,500 was invested at 13%.
$17,500 was invested at 4%
Explanation:
This is a simple interest problem.
The simple interest formula is given by:
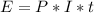
In which E is the amount of interest earned, P is the principal(the initial amount of money), I is the interest rate(yearly, as a decimal) and t is the time.
After t years, the total amount of money is:
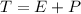
In this question:
Loans totaling 29,000.
P was invested at 13%
29000 - P was invested at 4%.
First investment:
Principal P.
Interest 13% = 0.13.
One year, so t = 1.
So
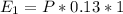
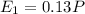
Second investment:
Principal 29000 - P.
Interest 4% = 0.04.
One year, so t = 1.
So
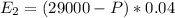
The total interest earned for both loans was $2,195.00.
This means that
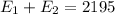
So
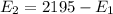
So we solve the following system:
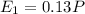
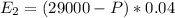
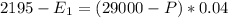
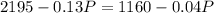
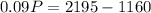
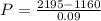

$11,500 was invested at 13%.
29000 - 11500 = 17500
$17,500 was invested at 4%