Answer:
They are perpendicular because they have slopes that are opposite reciprocals of −2 and .
Explanation:
The given lines are
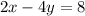
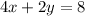
Let's rewrite each equation in the form
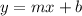
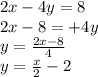
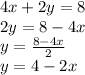
Now, let's use the perpendicular rule
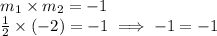
As you can observe, the slopes satisfy the perpendicular rule, that means the lines are perpendicular.
Therefore, the right answer is the second choice because it states the rule of perpendicularity between the given lines.