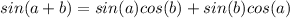Explain why you cannot use the Distributive Property to evaluate an expression in the form of sin(a + b). Please illustrate with an example along with your explanation.

Question

asked Jan 28, 2021 174k views

1 Answer

Niks · Answer 1 · 2021-02-03T20:15:08+0000

Answer:

The distributive property is to multiply the outside of a parenthesis by each term inside, for example:

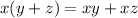
x(y+z)=xy+xz

this cannot be done with the trigonometric functions such as the sine.

An example of this:

let's prove that we don't get the correct result using the distributive property in the following expression:

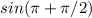$sin (\pi+\pi/2)$ ≠
$sin(\pi)+sin(\pi/2)$

We add the elements in the parentheses on the left side:

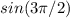$sin(3\pi/2)$ ≠
$sin(\pi)+sin(\pi/2)$

this are known values of the sine function:

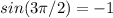
$sin(3\pi/2)=-1$

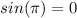
$sin(\pi)=0$

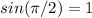
$sin(\pi/2)=1$

substituting these values we will get that:

-1 ≠ 0 +1

-1 ≠ 1

Thus we notice that we don't get the correct result using the distributive property.

The correct way to express the angle sum in the sine function is:

sin(a+b)=sin(a)cos(b)+sin(b)cos(a)