One way to do this is to exploit the Pythagorean identity,
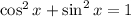
to rewrite
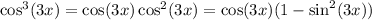
so that
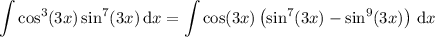
Then substitute
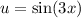 and
and
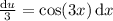 to get the integral
to get the integral
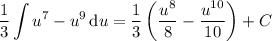
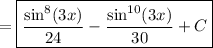
which is one correct form of the antiderivative. There's no reason we can't use the identity from before to express the integrand in terms of powers of cos(3x) instead.