Answer:

Explanation:
Please refer to attached for labeling of the diagram:
We have 2 triangles here in the figure:
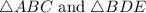 .
.
1.
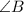 is common to both the triangles.
is common to both the triangles.
Sides AC || DE (parallel sides):
So, Corresponding angles will be equal
2.

3.
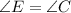
So,
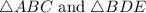 are similar to each other.
are similar to each other.
Similar triangles have ratio of their sides as equal.
So,
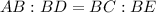

Hence,
