Question

Suppose that you are testing the hypotheses Upper H 0​: pequals0.16 vs. Upper H Subscript Upper A​: pnot equals0.16. A sample of size 350 results in a sample proportion of 0.21. ​a) Construct a 90​% confidence interval for p. ​b) Based on the confidence​ interval, can you reject Upper H 0 at alphaequals0.10​? Explain. ​c) What is the difference between the standard error and standard deviation of the sample​ proportion? ​d) Which is used in computing the confidence​ interval?

Answer 1

Given:

Sample size, n = 350

Sample proportion, P' = 0.21

H0 : p = 0.16

Ha : p ≠ 0.16

a) A 90% confidence interval for P.

Significance level = 1 - confidence interval = 1 - 0.90 = 0.10

For Z critical, we have:

Z critical =
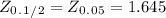`Z_0_._1_/_2 = Z_0_._0_5 = 1.645` (using z table)

Standard error, S.E =
`\sqrt{(P'(1 - P'))/(n)} = \sqrt{(0.21(1 - 0.21))/(350)} = 0.02177`

Margin of error, E = 1.645 * 0.02177 =0.03581

The 90% confidence interval =

0.21 ± 0.03581

The lower limit: 0.21 - 0.03581 = 0.17419

The upper limit: 0.21+0.03581 =0.24581

b) Based on the confidence interval at significance level = 0.10,

We reject null hypothesis, H0, since 0.16 is not cointained in the confidence interval. We conclude that p ≠ 0.16.

c) Standard error is based on sample proportion p^ while standard deviation is based on hypothesized proportion Po.

d) Standard error is used to compute the confidence interval.