Question

a boy is standing on a pole of height 14.7m throws a stone upwards. it moves in a vertical line slightly away from the pole and falls on the ground. its equation of motion in meters and seconds is x=9.8t-4.9t^2. find time taken for upward and downward motions. also find the maximum height reached by the stone from the ground.

Answer 1

The time taken for the upward motion is 1 second. The same time is taken for the downward motion

It reaches a maximum height of 4.9 meters.

Explanation:

The equation of motion is:

`x(t) = -4.9t^(2) + 9.8t`

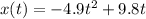
Since the term which multiplies t squared is negative, the graph is concave down, that is, x increases until the vertex, where it reaches it's maximum height, then it decreases.

Vertex of a quadratic equation:

Quadratic equation in the format
`x(t) = at^(2) + bt + c`

The vertex is the point
`(t_(v), x(t_(v)))`, in which

`t_(v) = -(b)/(2a)`

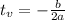
In this question:

`x(t) = -4.9t^(2) + 9.8t`

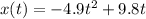
So
`a = -4.9, b = 9.8`

Vertex:

`t_(v) = -(9.8)/(2*(-4.9)) = 1`

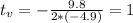
The time taken for the upward motion is 1 second.

`x(t_(v)) = x(1) = 9.8*1 - 4.9*(1)^(2) = 4.9`

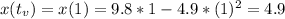
It reaches a maximum height of 4.9 meters.

Downward motion:

From the vertex to the ground.

The ground is t when x = 0. So

`-4.9t^(2) + 9.8t = 0`

`4.9t^(2) - 9.8t = 0`

`4.9t(t - 2) = 0`

`4.9t = 0`

`t = 0`

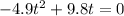
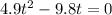
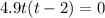
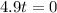
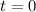
Or

`t - 2 = 0`

`t = 2`

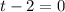
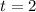
It reaches the ground when t = 2 seconds.

The downward motion started at the vertex, when t = 1.

So the duration of the downward motion is 2 - 1 = 1 second.