Question

Can someone help me with this question?

The one-year survival rate for pancreatic cancer is 20%. Of 12 people diagnosed with pancreatic cancer at one hospital, 6 survived one year. What is the probability of that happening.

Answer 1

The required probability is 0.0155.

Explanation:

We are given that the one-year survival rate for pancreatic cancer is 20%.

Of 12 people diagnosed with pancreatic cancer at one hospital, 6 survived one year.

The above situation can be represented through binomial distribution;

`P(X=r) = \binom{n}{r} * p^(r) * (1-p)^(n-r) ; x = 0,1,2,3,......`

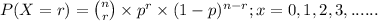
where, n = number of trials (samples) taken = 12 people

r = number of success = 6 survived

p = probability of success which in our question is probability of

one-year survival rate for pancreatic cancer, i.e; p = 20%

Let X = Number of people survived one year

So, X ~ Binom(n = 12 , p = 0.20)

Now, the probability that 6 survived one year is given by = P(X = 6)

P(X = 6) =
`\binom{12}{6} * 0.20^(6) * (1-0.20)^(12-6)`

=
`924 * 0.20^(6) * 0.80^(6)`

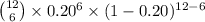
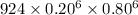
= 0.0155