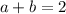Question

the graph of a line in the xy-plane slope 1/3 and contains the point (9,1). the graph of a second line passes through the points (-2,4) and (5,-3). if the two lines intersect at (a,b), what is the value of a+b?

Answer 1

`a + b = 2`

Step-by-step explanation:

The equations are determined by the definition of line equation:

First line

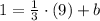`1 = (1)/(3)\cdot (9) + b` (Line equation)

`1 = 3 + b`

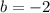`b = -2` (x-Intercept)

The equation of the first line is:

`y = (1)/(3)\cdot x - 2`

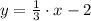
Second line

`m = ((-3)-4)/(5-(-2))`

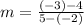
`m = - 1` (Slope)

`-3 = -1 \cdot (5)+b`

`-3 = -5 + b`

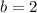`b = 2` (x-Intercept)

The equation of the second line is:

`y = -x + 2`

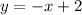
First, y is eliminated by equalization and x is found:

`(1)/(3)\cdot x -2 = -x +2`

`(4)/(3)\cdot x = 4`

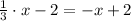
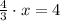
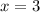`x = 3` (a)

Now, y is finally determined by direct substitution:

`y = -3+2`

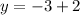
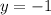`y = -1` (b)

The value of a + b is:

`a + b = 2`