Question

The reading speed of second grade students in a large city is approximately normal, with a mean of 90 words per

minute (wpm) and a standard deviation of 10 wpm. Complete parts (a) through (f).

-
(b) What is the probability that a random sample of 10 second grade students from the city results in a mean
reading rate of more than 96 words per minute?

The probability is ___
(Round to four decimal places as needed.)​

Answer 1

The probability that a random sample of 10 second grade students from the city results in a mean reading rate of more than 96 words per minute

P(x⁻>96) =0.0359

Explanation:

Explanation:-

Given sample size 'n' =10

mean of the Population = 90 words per minute

standard deviation of the Population =10 wpm

we will use formula

`Z = (x^(-)-mean )/((S.D)/(√(n) ) )`

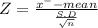
Let X⁻ = 96

`Z = (96-90 )/((10)/(√(10) ) )`

Z = 1.898

The probability that a random sample of 10 second grade students from the city results in a mean reading rate of more than 96 words per minute

`P(X^(-)>x^(-) ) = P(Z > z^(-) )`

= 1- P( Z ≤z⁻)

= 1- P(Z<1.898)

= 1-(0.5 +A(1.898)

= 0.5 - A(1.898)

= 0.5 -0.4641 (From Normal table)

= 0.0359

Final answer:-

The probability that a random sample of 10 second grade students from

= 0.0359