Question

Three long parallel wires, each carrying 20 A in the same direction, are placed in the same plane with the spacing of 10 cm. What is the magnitude of net force per metre on central wire?

Answer 1

F/L = 8*10^-4 N/m

Step-by-step explanation:

To calculate the magnitude of the force per meter in the central wire, you take into account the contribution to the force of the others two wires:

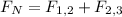`F_N=F_(1,2)+F_(2,3)` (1)

F1,2 : force between first and second wire

F2,3 : force between second and third wire

The force per meter between two wires of the same length is given by:

`(F)/(L)=(\mu_oI_1I_2)/(2\pi r)`

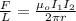
μo: magnetic permeability of vacuum = 4pi*10^-7 T/A

r: distance between wires

Then, you have in the equation (1):

`(F_N)/(L)=(\mu_oI_1I_2)/(2\pi r)+(\mu_oI_2I_3)/(2\pi r)\\\\(F_N)/(L)=(\mu_oI_1)/(2\pi r)[I_2+I_3]`

But

I1 = I2 = I3 = 10A

r = 10cm = 0.1m

You replace the values of the currents and the distance r and you obtain:

`(F_N)/(L)=(\mu_oI^2)/(\pi r)\\\\(F_N)/(L)=((4\pi*10^(-7)T/A)(20A)^2)/(2\pi (0.1m))=8*10^(-4)(N)/(m)`

hence, the net force per meter is 8*10^-4 N/m