Answer:
The probability that a randomly selected small cube is rolled and the face on the top is black is P=0.2.
Explanation:
We have a cube, with the faces painted black, that each side is divided in 5, so we end up with 125 cubes.
We have to calculate the probability that a randomly selected cube is rolled and the face on the top is black.
This probability is equal to the proportion of black area in the total area of the cube.
We can define the side of the original cube as A=5a, being a the side of the small cubes.
The area that is painted black is equal to the sum of 6 squares of side A. In terms of a, that is:
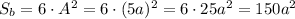
The total area of the 125 small cubes is:
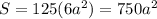
Then, the ratio of black surface to the total surface is:

Then, we can conclude that the probability that a randomly selected small cube is rolled and the face on the top is black is P=0.2.