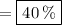The percent of container B that is left after pumping the water of Container A full in it is 40 per cent .
Step by step Step-by-step explanation :
Given -
- Two containers ( Container A & Container B ) in shape of cylinders.
- Diameter of Container A = 6 feet
- Height of Container A = 18 feet
- Diameter of container B = 8 feet
- Height of Container B = 17 feet
To find -
The percent of container B that is left after pumping the water of Container A full in it.
Solution -
Firstly, we have to find how much water each container can hold i.e. volume of containers .
We know that -
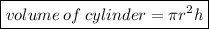
where, r is the radius of the cylinder & h is the height of the cylinder.
Now,
For Container A
Given, diameter = 6 feet
.•. Radius =
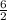
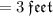
Height = 18 feet
•.• Volume of Container A =
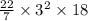
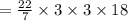
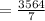
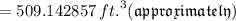
Rounding off to the nearest tenth . ..
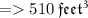
For Container B
Given, Diameter = 8 feet
.•. Radius =
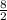

Height = 17 feet
•.• Volume of Container B =
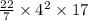
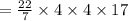
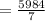
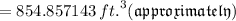
Rounding off to the nearest tenth. ..
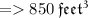
Now,
Volume container B that is left after pumping the water of Container A in it = Volume of Container B - Volume of Container A
= ( 850 - 510 ) ft^3
= 340 ft^3
Now ,
The percent of container B that is left after pumping the water of Container A in it = Volume container B that is left after pumping the water of Container A /Total volume of Container B × 100