Question

Water is added to a cylindrical tank of radius 5 m and height of 10 m at a rate of 100 L/min. Find the rate of change of the water level when the water is 6 m deep. (1 L = 1000cm^3)

Answer 1

`V = \pi r^2 h`

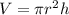
For this case we know that
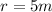`r=5m` represent the radius,
`h = 10m` the height and the rate given is:

`(dV)/(dt)= (100 L)/(min)`

`Q = 100 (L)/(min) *(1m^3)/(1000L)= 0.1 (m^3)/(min)`

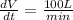
And replacing we got:

`(dh)/(dt)=(0.1 m^3/min)/(\pi (5m)^2)= 0.0012732 (m)/(min)`

And that represent
`0.127 (cm)/(min)`

Explanation:

For a tank similar to a cylinder the volume is given by:

`V = \pi r^2 h`

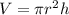
For this case we know that
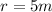`r=5m` represent the radius,
`h = 10m` the height and the rate given is:

`(dV)/(dt)= (100 L)/(min)`

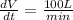
For this case we want to find the rate of change of the water level when h =6m so then we can derivate the formula for the volume and we got:

`(dV)/(dt)= \pi r^2 (dh)/(dt)`

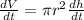
And solving for
`(dh)/(dt)` we got:

`(dh)/(dt)= ((dV)/(dt))/(\pi r^2)`

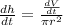
We need to convert the rate given into m^3/min and we got:

`Q = 100 (L)/(min) *(1m^3)/(1000L)= 0.1 (m^3)/(min)`

And replacing we got:

`(dh)/(dt)=(0.1 m^3/min)/(\pi (5m)^2)= 0.0012732 (m)/(min)`

And that represent
`0.127 (cm)/(min)`