Question

Point b has coordinates (-8,15) and lies on the circle whose equation is x^2+y^2=289. If an angles is drawn in standard position with its terminal ray extending through point b, what is the cosine of the angle?

Answer 1

`\cos \theta=-(8)/(17)`

Explanation:

Coordinates of Point b
`=(-8,15)`

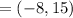
b lies on the circle whose equation is
`x^2+y^2=289`

`x^2+y^2=17^2`

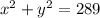
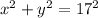
Comparing with the general form a circle with center at the origin:
`x^2+y^2=r^2`

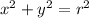
The radius of the circle =17 which is the length of the hypotenuse of the terminal ray through point b.

For an angle drawn in standard position through point b,

x=-8 which is negative

y=15 which is positive

Therefore, the angle is in Quadrant II.

`\cos \theta=(Adjacent)/(Hypotenuse) \\$Adjacent=-8\\Hypotenuse=17\\\cos \theta=(-8)/(17) \\\cos \theta=-(8)/(17)`