What is the y-coordinate of the point that divides the directed line segment from J to K into a ratio of 2:3? K(8,11) J(-3,1) 7 -6 5 -5

Question

asked Jan 3, 2021 121k views

2 Answers

Nick Farina · Answer 1 · 2021-01-08T05:02:42+0000

Answer:

(D)5

Explanation:

Given the point J(-3,1) and K(8,11).

The line segment that divides the segment from J to K in any given ratio can be determined using the formula.

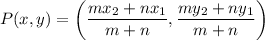
$P(x,y)=\left((mx_2+nx_1)/(m+n) ,(my_2+ny_1)/(m+n)\right)$

In the given case:

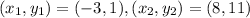(x_1,y_1)=(-3,1), (x_2,y_2)=(8,11) , m:n=2:3

Since we are to determine the y-coordinate of the point that divides JK into a ratio of 2:3, we have:

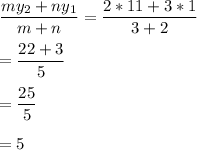
$(my_2+ny_1)/(m+n)=(2*11+3*1)/(3+2)\\\\=(22+3)/(5)\\\\=(25)/(5)\\\\=5$

The y-coordinate of the point that divides the directed line segment from J to K into a ratio of 2:3 is 5.

The correct option is D.