Question

When Colton commutes to work the amount of time it takes him to arrive is normally distributed with a mean of 41 minutes and a standard deviation of three minutes what percentage of his commute will be between 33 and 35 minutes to the nearest tenth?

Answer 1

The Probability that commute will be between 33 and 35 minutes to the nearest tenth = 0.0189 ≅1.89%

Explanation:

Step(i):-

Given mean of the Population(μ) = 41 minutes

Given standard deviation of the Population (σ) = 3 minutes

let 'X' be the random variable of Normal distribution

Let X = 33

`Z = (x -mean)/(S.D) =(33-41)/(3) = -2.66`

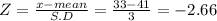
let X = 35

`Z = (x -mean)/(S.D) =(35-41)/(3) = -2`

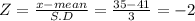
Step(ii):-

The Probability that commute will be between 33 and 35 minutes to the nearest tenth

P(33≤ X≤35) = P(-2.66 ≤X≤-2)

= P( X≤-2) - P(X≤-2.66)

= 0.5 - A(-2) - (0.5 - A(-2.66)

= 0.5 -0.4772 - (0.5 -0.4961) (From normal table)

= 0.5 -0.4772 - 0.5 +0.4961

= 0.4961 - 0.4772

= 0.0189

The Probability that commute will be between 33 and 35 minutes to the nearest tenth = 0.0189 ≅1.89%