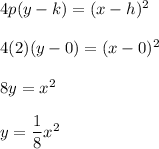Question

Which is the equation of a parabola with vertex (0,0) and focus (0,2)?

Answer 1

The equation of the parabola is y=(1/8)x^2

`y=(1)/(8)x^2`

Explanation:

We know the vertex (0,0) and the focus (0,2) of the parabola.

The equation in vertex form is written as:

`y=a(x-h)^2+k\\\\\text{vertex}=(h,k)`

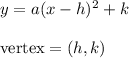
Then, in this case, we have the equation:

`y=a(x-0)^2+0=ax^2`

As the focus is (0,2), it is at a distance of 2 units from the vertex (0,0).

For the focus, we have the following equation:

`4p(y-k)=(x-h)^2`

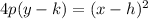
where p is the distance from the focus to the vertex (in this case, p=2).

h and k are the vertex coordinates, both 0.

So we have:

`4p(y-k)=(x-h)^2\\\\4(2)(y-0)=(x-0)^2\\\\8y=x^2\\\\y=(1)/(8)x^2`