Question

Which is the equation of a hyperbola centered at the origin with x-intercept +\- 3 and asymptote y=2x

Answer 1

Answer: c

Step-by-step explanation: edge 23

Answer 2

`{(x^(2))/(9) - (y^(2))/(36) = 1}`

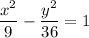
Explanation:

The hyperbola has x-intercepts, so it has a horizontal transverse axis.

The standard form of the equation of a hyperbola with a horizontal transverse axis is
`((x - h)^(2))/(a^(2)) - ((y - k)^(2))/(b^(2)) = 1`

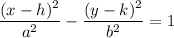
The center is at (h,k).

The distance between the vertices is 2a.

The equations of the asymptotes are
`y = k \pm (b)/(a)(x - h)`

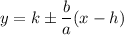
1. Calculate h and k. The hyperbola is symmetric about the origin, so

h = 0 and k = 0

2. For 'a': 2a = x₂ - x₁ = 3 - (-3) = 3 + 3 = 6

a = 6/2 = 3

3. For 'b': The equation for the asymptote with the positive slope is

`y = k + (b)/(a)(x - h) = (b)/(a)x`

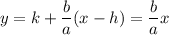
Thus, asymptote has the slope of

`\begin{array}{rcl}m& =& (b)/(a)\\\\2& =& (b)/(3)\\\\b& =& \mathbf{6}\end{array}`

4. The equation of the hyperbola is

`\large \boxed{\mathbf{(x^(2))/(9) - (y^(2))/(36) = 1}}`

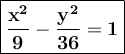
The attachment below represents your hyperbola with x-intercepts at ±3 and asymptotes with slope ±2.