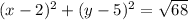Question

A circle has a center located at 2 5 and passes through the point 10 3 answer

Determine the equation of the circle. Show how you arrived at your answer.
Write the equation of the tangent line to the circle at the point . Show how you determined your answer.

Answer 1

`(x-2)^(2) +(y-5)^(2) =√(68)`

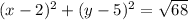
Explanation:

Givens

• The center of the circle is at (2,5).
• A point on the circumference is at (10,3).

First, we need to find the radius, which is the distance between the given points.

`d=\sqrt{(3-5)^(2) +(10-2)^(2) } =√(4+64)=√(68)`

Therefore, the radius of the circle is

`r \approx 8.25`

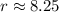
The explicit form of the equation of the circle would be

`(x-2)^(2) +(y-5)^(2) =√(68)`