Question

Li is using a cone shaped cup with a diameter of 7 and 3/8 cm and a height of 10 cm. Find the total volume of the cup. Round to the nearest tenth.

Answer 1

The volume of the cup is of 142.2 cubic centimeters.

Explanation:

The cone volume is given by the following equation:

`V = (\pi r^(2)h)/(3)`

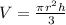
In which r is the radius, which is half the diameter, and h is the height.

In this question:

Dimensions in cm, so the volume will be in cubic centimers.

Height of 10 cm, so
`h = 10`

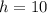
Diameter of
`7 + (3)/(8) = (7*8 + 3)/(8) = (59)/(8) = 7.375`

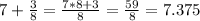
So the radius is
`r = (7.375)/(2) = 3.6875`

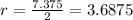
Volume of the cup:

`V = (\pi*(3.6875)^(2)*10)/(3) = 142.4`

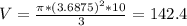
The volume of the cup is of 142.2 cubic centimeters.