Question

Which statement(s) can be interpreted from the equation for a real estate value, V 228,000(1.03)' where V) represents the value of the real estate and t represents the time in years?

The equation is an exponential growth equation

The equation is an exponential decay equation

The equation is neither exponential decay nor exponential growth

$228.000 represents the initial cost of a real estate that appreciates 3% per year over the course of years

$228.000 represents the initial cost of a real estate that appreciates 30% per year over the course of years

$228.000 represents the initial cost of a real estate that depreciates 3% per year over the course of t years

$228.000 represents the initial cost of a real estate that depreciates 30% per year over the course of years

Answer 1

The statements that are true for this equation are:

- The equation is an exponential growth equation.

- $228.000 represents the initial cost of a real estate that appreciates 3% per year over the course of years.

Explanation:

We have the equation

`V= 228,000(1.03)^t`

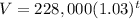
Where V: value of the real state and t: time in years.

As t is always positive in this case, and 1.03 is larger than 1, the value V will rise exponentially. The equation is an exponential growth equation.

The difference in value for each year is:

`(V_(t+1))/(V_t)=(1.03^(t+1))/(1.03^t)=1.03^(t+1-t)=1.03\\\\\\V_(t+1)-V{t}=1.03V_t-V_t=0.03V_t`

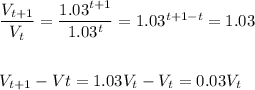
We can conclude that the value increases each year 0.03 (3%) from the previous year value, starting from $228,000 in the year t=0.

$228.000 represents the initial cost of a real estate that appreciates 3% per year over the course of years.