Question

A local kids play sold 8 adult tickets and 9 child tickets for a total of $205. On day two they sold only 4 adult tickets and 3 child tickets for a total of $83. What was the price of each kind of ticket?

Answer 1

Adult tickets cost $11 and child tickets cost $13

Explanation:

Multiply the second equation by -2, then add the equations together.

(8a+9c=205)

−2(4a+3c=83)

Becomes:

8a+9c=205

−8a−6c=−166

Add these equations to eliminate a:

3c = 39

Then solve3c=39for c:

3c=39

`(3c)/(3)` =
`(39)/(3)`

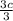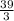
(Divide both sides by 3)

c = 13

Now that we've found c let's plug it back in to solve for a.

Write down an original equation:

8a+9c=205

Substitute 13 for c in 8a+9c=205:

8a+(9)(13)=205

8a+117=205 (Simplify both sides of the equation)

8a+117+−117=205+−117 (Add -117 to both sides)

8a=88

`(8a)/(8)` =
`(88)/(8)`

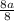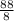
(Divide both sides by 8)

a = 11