Question

Please help!

You pick a card at random. Without putting the first card back, you pick a second card at random.

What is the probability of picking an even number and then picking an even number?

Simplify your answer and write it as a fraction or whole number.

Answer 1

Probability of picking an even and then even number =
`(1)/(6)`

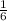
Explanation:

Probability of picking a card with even number,

P(even 1) =
`\frac{\text{favorable outcomes}}{\text{Total outcomes}}` =
`\frac{\text{even cards}}{\text{Total number of cards}}`

=
`(2)/(4)`

=
`(1)/(2)`

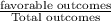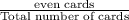
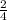
Followed by picking a card which is even without putting the first card back.

So an even card is to be picked out of remaining 3 cards.

P(even 2) =
`\frac{\text{favorable outcomes}}{\text{Total outcomes}}`

=
`(1)/(3)`

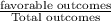
Now probability of both events = P(even 1) × P(even 2)

=
`(1)/(2)* (1)/(3)`

=
`(1)/(6)`

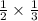
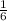
Therefore, probability of both the events will be
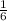`(1)/(6)`.