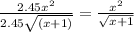Answer:
a)
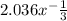
b)
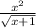
Explanation:
For a cube, all the sides are equal. Let the length of each side be L
a) The volume of a cube (V) = L³
For the first cube:
V = 270x in³
270x = L³
L = ∛(270x) =
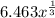
For the second cube:
V = 32x² in³
32x² = L³
L = ∛(32x²) =
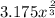
Ratio of length =
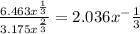
b) The surface area of a cube (s) = 6L²
For the first cube:
s = 6x⁴ ft²
6x⁴ = L²
L = √6x⁴= 2.45x²
For the second cube:
s = 6(x + 1) ft²
6(x + 1) = L²
L = √6(x + 1)= 2.45√(x + 1)
Ratio of the length =