Question

PLEASE HELP ME with an explanation. Thanks in advance

Answer 1

3) 0.30

The probability a randomly selected student plays a sport given they work part time = 0.30

Explanation:

Step(i):-

Given 'A' plays a sport

B work part time

Given P(A) = 0.48

P(B) = 0.40

P(A∩B) =0.12

P(A∪B)¹ =0.24

Step(ii):-

By using conditional probability

`P(B/A) = (P(BnA)/(P(A))`

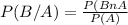
and similarly
`P(A/B) = (P(AnB)/(P(B))`

The probability a randomly selected student plays a sport given they work part time

Now
`P(A/B) = (P(AnB)/(P(B))`

`P(A/B) = (0.12)/(0.40)= 0.30`

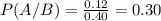
Final answer:-

The probability a randomly selected student plays a sport given they work part time = 0.30