Question

Two cylinders are made of the same material. Cylinder A is one-fourth (1/4) the length of cylinder B and it has a radius that is four times greater than the radius of cylinder B. What is the ratio of the mass of cylinder A to the mass of cylinder B?

Answer 1

4.

Step-by-step explanation:

Hello,

In this case, since we are talking about the same material, their densities are the same:

`\rho _A=\rho _B`

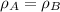
And each density is defined by:

`\rho _A=(m_A)/(V_A) \\\\\rho _B=(m_B)/(V_B)`

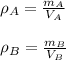
Thus, we also define the volume of a cylinder:

`V_(cylinder)=\pi r^2h`

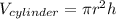
Therefore, we obtain:

`\rho _A=(m_A)/(\pi r_A^2h_A)`

`\rho _B=(m_B)/( \pi r_B^2h_B)`

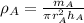
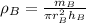
Now, the given information regarding the the length and the radius is written mathematically:

`h_A=(1)/(4) h_B\\\\r_A=4 r_B`

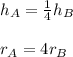
So we introduce such additional equations in:

`(m_A)/(\pi r_A^2h_A)=(m_B)/(\pi r_B^2h_B)\\\\(m_A)/(\pi (4r_B)^2((1)/(4)h_B))=(m_B)/(\pi r_B^2h_B)\\\\(m_A)/(m_B) =(\pi (4r_B)^2((1)/(4)h_B))/(\pi r_B^2h_B)`

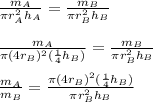
So we simplify for the radius and lengths:

`(m_A)/(m_B) =(\pi (4r_B)^2((1)/(4)h_B))/(\pi r_B^2h_B)\\\\(m_A)/(m_B) =16 *(1)/(4)\\ \\(m_A)/(m_B) =4`

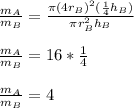
So the ratio of the mass of cylinder A to the mass of cylinder B is 4.

Best regards.

Answer 2

`M_(A)` :
`M_(B)` = 4 : 1

Step-by-step explanation:

Given that:

Volume of a cylinder =
`\pi`
`r^(2)`h

For cylinder A,
`l_(A)` =
`h_(A)` =
`(1)/(4) l_(B)` and
`r_(A)` = 4
`r_(B)`.

Volume of cylinder A =
`\pi`
`(4r_(B)) ^(2)` ×
`(1)/(4) l_(B)`

= 4
`\pi`
`r_(B) ^(2)`
`l_(B)`

Volume of cylinder B =
`\pi`
`(r_(B)) ^(2)`
`l_(B)`

=
`\pi`
`r_(B) ^(2)`
`l_(B)`

To determine the ratio of their masses, density (ρ) is defined as the ratio of the mass (M) of a substance to its volume (V).

i.e ρ =
`(M)/(V)`

Thus, since the cylinders are made from the same material, they have the same density (ρ). So that;

density of A = density of B

density of A =
`(M_(A) )/(4\pi r_(B) ^(2)l_(B) )`

density of B =
`(M_(B) )/(\pi r_(B) ^(2)l_(B) )`

⇒
`(M_(A) )/(4\pi r_(B) ^(2)l_(B) )` =
`(M_(B) )/(\pi r_(B) ^(2)l_(B) )`

The ratio of mass of cylinder A to that of B is given as;

`(M_(A) )/(M_(B) )` =
`(4\pi r_(B) ^(2) l_(B) )/(\pi r_(B) ^(2) l_(B) )`

⇒
`(M_(A) )/(M_(B) )` =
`(4)/(1)`

Therefore,
`M_(A)` :
`M_(B)` = 4 : 1