Answer:
The other endpoint of the segment is
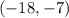 .
.
Explanation:
The midpoint of the points
 and
and
 is given by the following formula:
is given by the following formula:
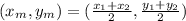
where
 = coordinates of the midpoint.
= coordinates of the midpoint.
We know that the midpoint is (-15, 2) and an endpoint is (-12, 11). Substituting the information we have gives:
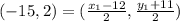
To find
 we need to solve this equation:
we need to solve this equation:
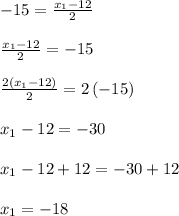
and to find
 we need to solve this equation:
we need to solve this equation:
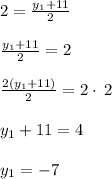
The other endpoint of the segment is
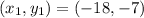 .
.