Answer:
The multiplicity of the root is 2
Explanation:
Multiplicity of a number is the number of times the factor of a given function appears in the factor form of such given equation. For us to know the multiplicity of the root of the function, first we must know its root.
Factorizing the given quadratic function x²−8x+16=0
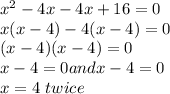
Since the root of the function which is 4 appears twice then the multiplicity of the root is 2