Answer:
The volume is 997.62 cubic units..
Explanation:
We are given the following details:
The pyramid has a regular hexagonal base i.e. each side of hexagon is equal.
Side of hexagonal base, a = 8 units
Altitude of pyramid, h = 18 units
We have to find the volume of pyramid.
Formula:

Where, B is the area of base of pyramid.
h is the height/altitude of pyramid
To calculate B:
Here, base is a hexagon with side 8 units.

Here, a = 8 units
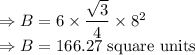
Putting values of B and h in Formula of volume:
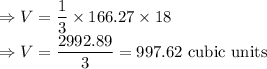
Hence, the volume is 997.62 cubic units.