Question

Solve one, any question you want, please show work,

Answer 1

Step 1: Variables are q for quarters and d for dimes. So d = dimes and q = quarters

Step 2: The two equations that form a system of equations are:

`\left \{ {{0.1d+.25q=3.70} \atop {d+q=19}} \right.`

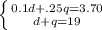
Step 3: Work is shown on the attachment and on the step-by-step explanation

Step 4: Given the context of the problem, the solution of the amount of dimes and quarters, which is 7 dimes and 12 quarters, is needed to satisfy both systems to concur that there was 7 dimes and 12 quarters in a sum of money that amounted to $3.70 with 19 coins in total.

Explanation:

Step 1: To first attempt to solve this, we must have to set up two variables for the amount of value a quarter and a dime has. So since a quarter is worth 0.25¢ in and a dime is worth 0.10¢, then we can set up one of the equations to be:

`0.1d + .25q = 3.70`

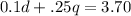
And we set it to equal the $3.70 because that's the amount that the sum of money totals to.

Step 2: Now to get the other side of the equation, we use the variables again, d and q and set that to equal 19 because that is the amount of coins that there is in total.

Step 3: Now that we have both equations, we can solve the problem now.

`\left \{ {{0.1d+.25q=3.70} \atop {d+q=19}} \right.`

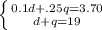
Let's first solve this equation by setting one of the side's variables the same absolute value, but not the same integer value so that we can cross it off. I will choose the equation
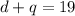`d+q=19` to be multiplied by -.1 so that we can cross off both 0.1d and -0.1d after the result of the multiplication:

`\left \{ {{0.1d+.25q=3.70} \atop {-.1d+-.1q=-1.9}} \right.`

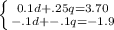
Now, lets cross off everything that we can, and add up the variables together. This includes adding .25q + (-.1q) and adding 3.70 + -1.9.

Now we have:

`\left \{ {{.25q=3.70} \atop {-.1q=-1.9}} \right.`

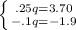
Now, what we do from here is add the left side and the right side side to get one equation, which is:

`.15q=1.8`

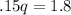
Finally, we divide both sides to get q=12, which means that there are 12 quarters. Since there are 19 coins in total, we can subtract 12 from 9 to get the remaining amount of dimes, which is 7.

In conclusion, q=12 and d=7.

My written work is also provided in the attachment!!!

Step 4: What does this mean in the context of the question?

This basically means that the solution of the amount of dimes and quarters, which is 7 dimes and 12 quarters, is needed to satisfy both systems to concur that there was 7 dimes and 12 quarters in a sum of money that amounted to $3.70 with 19 coins in total.

In simpler terms, this means that we need 7 dimes and 12 quarters to satisfy that there was a sum of money that amounted to $3.70 with 19 coins in total .