Answer: 14 feet
=======================================================
Step-by-step explanation:
Let C be the corner point.
x = distance from P to C
That makes segment AP to be 70-x feet long
Focus on the right triangle PBC. Use the pythagorean theorem to find the hypotenuse PB.

If we knew what x was, then we could find a numeric value for PB.
---------------------
It costs $28 per foot to run cable along the ground. This is the portion from A to P. So it costs 28(70-x) dollars to run that portion of cable above ground. Simply multiply the cost per foot by the number of feet.
Similarly, the cost from P to B is
 since it costs $53 per foot to have it run underground.
since it costs $53 per foot to have it run underground.
The total cost is therefore
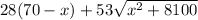
The derivative of this will help determine when the cost is minimized.
Type that function into GeoGebra and have it compute the derivative.
You should find that the x intercept of the derivative curve is exactly x = 56
If x = 56, then 70-x = 70-56 = 14
This means AP = 14 feet is the amount of cable to run along main street.
This also leads to
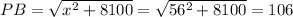
The total length of the wire is 14+106 = 120 feet
It costs $28 per foot along the 14 ft section, so 28*14 = 392 dollars is the cost for this section.
It costs $53 per foot along the 106 ft section, so 53*106 = 5618 dollars is the cost for this other section.
The total min cost is 392+5618 = 6010 dollars
------------------
Side note: You could do all this without a calculator to compute the derivative and use algebra to end up with x = 56. However, I think the use of technology is beneficial because it's fast/efficient. In real world settings, you won't be likely to pull out pencil/paper to get things done. The modern world relies on computers. It's refreshing to see that your teacher encourages the use of technology.
Let me know if you need me to go over the algebraic steps and I'll update my answer.