Question

A simple hydraulic lift is made by fitting a piston attached to a handle into a 3.0-cm diameter cylinder. The cylinder is connected to a larger cylinder with a 24-cm diameter. If a 50-kg woman puts all her weight on the handle of the smaller piston, what weight could the other piston lift?

Answer 1

Approximately
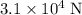`3.1 * 10^4 \; \rm N` (assuming that the acceleration due to gravity is
`g = 9.81\; \rm kg \cdot N^(-1)`.)

Step-by-step explanation:

Let
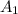`A_1` denote the first piston's contact area with the fluid. Let
`A_2` denote the second piston's contact area with the fluid.

Similarly, let
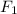`F_1` and
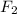`F_2` denote the size of the force on the two pistons. Since the person is placing all her weight on the first piston:

`F_1 = W = m \cdot g = 50\; \rm kg * 9.81 \; \rm kg \cdot N^(-1) =495\; \rm N`.

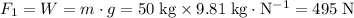Since both pistons fit into cylinders, the two contact surfaces must be circles. Keep in mind that the area of a square is equal to
`\pi` times its radius, squared:

• 
  `\displaystyle A_1 = \pi * \left((1)/(2) * 3.0\right)^2 = 2.25\, \pi\;\rm cm^(2)`.
• 
  `\displaystyle A_2 = \pi * \left((1)/(2) * 24\right)^2 = 144\, \pi\;\rm cm^(2)`.

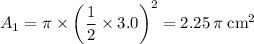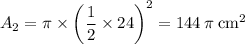By Pascal's Law, the pressure on the two pistons should be the same. Pressure is the size of normal force per unit area:

`\displaystyle P = (F)/(A)`.

For the pressures on the two pistons to match:

`\displaystyle (F_1)/(A_1) = (F_2)/(A_2)`.

`F_1`,
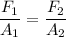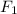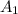`A_1`, and
`A_2` have all been found. The question is asking for
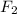`F_2`. Rearrange this equation to obtain:

`\displaystyle F_2 = (F_1)/(A_1) \cdot A_2 = F_1 \cdot (A_2)/(A_1)`.

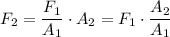Evaluate this expression to obtain the value of
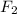`F_2`, which represents the force on the piston with the larger diameter:

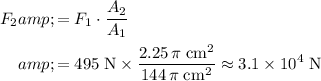`\begin{aligned}F_2 &= F_1 \cdot (A_2)/(A_1) \\ &= 495\; \rm N * (2.25\, \pi\; \rm cm^2)/(144\, \pi \; \rm cm^2) \approx 3.1 * 10^4\; \rm N\end{aligned}`.