Answer:
D. 1
Explanation:
To solve this problem, we just need to find the common point of these linear function, beacuse they form a piecewise function which is continuous according to the problem, that means they are related by one common point.
Let's solve the following expression
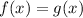 , where
, where
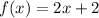 and
and
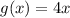 . So,
. So,
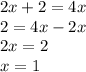
Which means
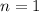 , that is, if the n is greater than 1, then the function is defined by
, that is, if the n is greater than 1, then the function is defined by
 , if the n is least or equal than 1, then the functioni is defined by
, if the n is least or equal than 1, then the functioni is defined by

Therefore, the right answer is D.