Answer:
Given:
Sample size, n = 6965
Sample proportion p' =
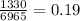
Let's claim that the return rate is less than 20%, ie, P = 0.2
Significance level = 0.01
The null and alternative hypotheses:
H0 : P = 0.2
H1 : P < 0.2
Option A is correct
_____________________________
For the test statistic, Z, let's use the formula:
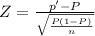
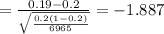
Z = -1.887 ≈ -1.89
___________________________
The p-value.
This is a left tailed test.
Using z table,
P-value = P(Z ≤ -1.89) = 0.029
The pvalue is 0.029
Decision:
Because the pvalue, 0.029 is greater than level of significance, 0.01, we fail to reject null hypothesis, H0.
Conclusion:
There is not enough sufficient evidence to conclude that the return rate is less than 20%