Question

Radar consists of electromagnetic waves. A warplane is rendered invisible to enemy radar by applying an antireflective polymer coating. If radar waves have a frequency of 10 GHz (Giga = 1E9), and the index of refraction of the polymer for these waves is 1.50, what is the minimum thickness of the antireflective coating? (c = 3E8 m/s. The index of refraction of air is ~1, and that of the fuselage is larger than for the polymer coating)

Answer 1

d = 0.015m

Step-by-step explanation:

To find the thickness of the antireflective coating you take into account that waves must reflect and interfere destructively between them. A wave travels twice the thickness d of the coating, and for the destructive interference it is necessary that the reflected wave is (m+1/2) factor of the incident wave. Thus, you have:

`2d=(m+(1)/(2))\lambda_n`

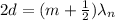
d: thickness of the coating

m: order of the interference (m=1 for the minimum thickness)

λn: wavelength of light inside the coating

You first calculate the wavelength of the wave:

`\lambda=(c)/(f)=(3*10^8m/s)/(10*10^9Hz)=0.03m`

`\lambda_(coating)=\lambda_n=(n_(air))/(n_(coating))\lambda_(air)\\\\\lambda_n=(1)/(1.50)(0.03m)=0.06m`

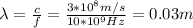
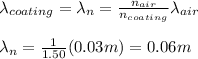
Then, you replace the values of m and λn in order to calculate d:

`d=(1)/(2)(m+(1)/(2))\lambda_n`

`d=(1)/(2)(0+(1)/(2))(0.06m)=0.015m=1.5cm`

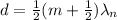
hence, the thickness of the antireflective coating must be 0.015m