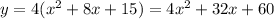Answer:
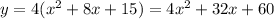
Explanation:
A parabola has the following format:
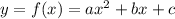
If a is positive, it's minium value is:

In which

Factoring:
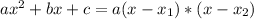 , in which
, in which
 are the intercepts.
are the intercepts.
In this question:
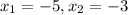
So
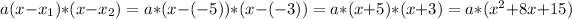
Suppose a = 1, we have:
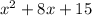
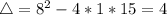
The minimum value will be:
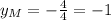
We want this minimum value to be -4, which is 4 times the current minimum value, so we need to multiply a by 4. Then
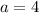
And the parabola is: