Question

If Mario puts $12,000 in a bank account that pays 4% interest quarterly, how much will he have after 3 years?

Answer 1

`P=12000, r= 0.04, t=3`

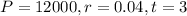
And n=4 since the rate is compounded quarterly, so then replacing this info we got:

`A = 12000 (1+ (0.04)/(4))^(4*3) = 13521.9`

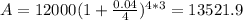
So then Mario will have about $13521.9 after the 3 years with the rate of interest used.

Explanation:

For this case we can use the formula for future value based on a compound interest given by:

`A= P (1+ (r)/(n))^(nt)`

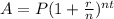
Where A represent the future value, P the present value or the inversion r is the rate of interest on fraction, n the number of times that the rate of interest is compounded in a year and t the number of years.

For this case we know this:

`P=12000, r= 0.04, t=3`

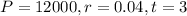
And n=4 since the rate is compounded quarterly, so then replacing this info we got:

`A = 12000 (1+ (0.04)/(4))^(4*3) = 13521.9`

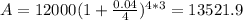
So then Mario will have about $13521.9 after the 3 years with the rate of interest used.