Question

A 2.0 c charge moves with a velocity of (2.0i+4.0j+6.0k)m/s and experiences a magnatic force of (0.4i-20j+12k)N. The x component of the magnatic field is equal to zero. Determine the y component of the magnatic field

Answer 1

-0.033 units

Step-by-step explanation:

According to Lorentz force law, the magnetic force, F, on a moving charge, q, moving with a velocity, v, in a magnetic field, B, is given by;

F = q v x B ----------------(i)

Where;

F, v and B are vectors. Therefore, equation (i) represents a vector product of the velocity and magnetic field vectors.

From the question;

v = (2.0i + 4.0j + 6.0k)m/s

F = (0.4i - 20j + 12k)N

q = 2.0C

Let the magnetic field vector be given by;

B = ai + bj + ck ---------------------(*)

Where;

a, b and c are the magnitudes of the x, y and z components of the magnetic field.

Substitute the values of F, v, B and q into equation (i) as follows;

(0.4i - 20j + 12k) = 2.0(2.0i + 4.0j + 6.0k) x (ai + bj + ck)

Expanding the second bracket gives

(0.4i - 20j + 12k) = (4.0i + 8.0j + 12.0k) x (ai + bj + ck) ---------------(ii)

Solving the right hand side of equation (ii) which is the vector product gives;

| |

| i j k |

(0.4i - 20j + 12k) = | 4.0 8.0 12.0 |

| a b c |

| |

(0.4i - 20j + 12k) = (8.0c - 12.0b)i - (4.0c -12.0a)j + (4.0b - 8.0a)k ----(iii)

Comparing both sides of equation (iii) gives the following three equations;

0.4 = 8.0a - 12.0b --------------------(iv)

-20 = 4.0c - 12.0a ---------------------(v)

12 = 4.0b - 8.0a ----------------------(vi)

From the question, it is given that the x component of the magnetic field is equal to zero. Now, recall that from equation (*) above, the magnitude of the x-component of the magnetic field is given as a

Therefore;

a = 0

To get the y component, which is b, substitute the value of a = 0 into equation (iv) as follows;

0.4 = 8.0(0) - 12.0b

0.4 = 0 - 12.0b

0.4 = - 12.0b

Solve for b;

b =
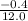`(-0.4)/(12.0)` = -0.033

Therefore the y component of the magnetic field is -0.033 units

Answer 2

`\vec{B}_(y)=6T`

Step-by-step explanation:

Here we can use the Lorentz force equation.

`\vec{F}_(B)=q(\vec{v}* \vec{B})`

We know:

• v is the velocity (2.0i+4.0j+6.0k) m/s
• F is the magnetic force (0.4i-20j+12k) N
• B is the magnetic force (ai+bj+ck) T
• q is the charge 2 C

So we will have:

`(0.4i-20j+12k)=2((2.0i+4.0j+6.0k) * (ai+bj+ck))`

Let's solve the cross product, knowing that x component of B is 0, it means a=0.

`(0.4i-20j+12k)=2((2.0i+4.0j+6.0k) * (0i+bj+ck))`

`(0.4i-20j+12k)=2((4c-6b)i-2cj+2bk)`

Comparing the k component we have:

`12=2b`

`b=6`

If we see b is the y-component of the magnetic field, therefore
`\vec{B}_(y)=6T`

I hope it helps you!