Question

A row of tiny red beads is placed at the beginning and at the end of a 20‐centimeter bookmark.

A row of the same beads is also placed every 4 millimeters along the bookmark.
How many rows of the beads are used on the bookmark?

Answer 1

51 rows

Explanation:

Given

Length of bookmark = 20cm

Distance between beads = 4mm

Required

Number of rows of beads

First, the distance between the rows of beads must be converted to cm

if 1mm = 0.1cm

then

4mm = 4*0.1cm

4mm = 0.4 cm

This means that each row of beads is placed at 0.4 cm mark.

The distance between each row follows an arithmetic progression and it can be solved as follows;

`T_n = a + (n-1)d`

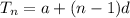
Where
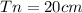`Tn = 20cm` (The last term)

`a = 0 cm` (The first term)

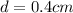`d = 0.4cm` (The distance between each row of beads)

n = ?? (number of rows)

Solving for n; we have the following;

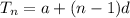`T_n = a + (n-1)d` becomes

`20 = 0 + (n-1)0.4`

`20 = (n-1)0.4`

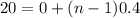
DIvide both sides by 0.4

`(20)/(0.4) = ((n-1)0.4)/(0.4)`

`50 = (n-1)`

`50 = n-1`

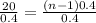
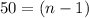
Add 1 to both sides

`50 + 1= n-1 + 1`

`n = 51`

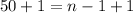
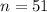
Hence, the number of rows of beads is 51