Answer:
The alternate exterior angles with angle 11 are angle 13 and angle 5.
Explanation:
Two angles are called Alternate exterior angles if
1. They are on the exterior side of parallel lines and
2. Lie on the opposite sides of the transversal line.
It is given that
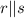 and
and
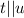
From the figure it is noticed that the angle 13 and angle 5 are on the exterior side of parallel lines and they lie on the opposite sides of the transversal line.
Therefore alternate exterior angles with angle 11 are angle 13 and angle 5.