Question

A piecewise function f(x) is defined as shown. f(x) = StartLayout enlarged left-brace 1st Row 1st column negative five-fourths x + 90, 2nd column 0 less-than-or-equal-to x less-than 40 2nd row 1st column negative three-eighths x + 75, 2nd column 40 less-than-or-equal-to x less-than-or-equal-to 200 EndLayout Which table could be used to graph a piece of the function? A 2-column table has 3 rows. The first column is labeled x with entries 0, 16, 40. The second column is labeled y with entries 90, 85, 75. A 2-column table has 3 rows. The first column is labeled x with entries 0, 40, 200. The second column is labeled y with entries 90, 40, 0. A 2-column table has 3 rows. The first column is labeled x with entries 40, 120, 200. The second column is labeled y with entries 75, 30, 0. A 2-column table has 3 rows. The first column is labeled x with entries 40, 160, 200. The second column is labeled y with entries 60, 15, 0.

Answer 1

D

Explanation:

edge2020

Answer 2

(D)The first column is labeled x with entries 40, 160, 200. The second column is labeled y with entries 60, 15, 0.

Explanation:

The piece-wise function, f(x) is defined as follows:

`f(x)=\left\{\begin{array}{ccc}-(5)/(4)x+90 &0\leq x<40\\\\-(3)/(8)x+75 &40\leq x\leq 200\end{array}\right`

`f(0)=-(5)/(4)*0+90=90\\\\f(16)=-(5)/(4)*16+90=70\\\\f(40)=-(3)/(8)*40+75=60\\\\f(120)=-(3)/(8)*120+75=30\\\\f(160)=-(3)/(8)*160+75=15\\\\f(200)=-(3)/(8)*200+75=0`

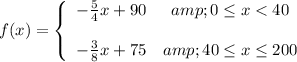
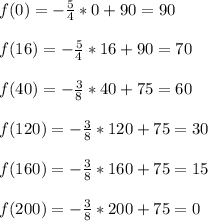
Therefore, the table which could represent the function is that which satisfies the points above.

In option D

`\left|\begin{array}cx&f(x)\\--&--\\40&60\\160&15\\200&0\end{array}\right|`

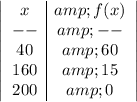
The correct option is D