Question

Super Dave Osborne stands at the bottom of a canyon elevation 256 feet below sea level, he throws a piano up at a velocity of 320 feet per second the piano lands on the edge of the cliff at zero elevation . The flight of the piano is modeled by the equation f( x ) = −16t2 2 + 320t − 256. The piano was in the air for exactly how many seconds

Answer 1

The piano was in the air for 18.34 seconds.

Explanation:

The height of the piano after t seconds is given by the following equation:

`f(t) = -16t^(2) + 320t - 256`

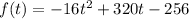
Initially, the piano is below the ground level. At the first root of the equation, it will go into the air, and then some time after that it will fall down again, which is at the second root of the equation.

Roots of a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

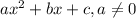This polynomial has roots
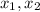`x_(1), x_(2)` such that
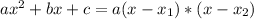`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\bigtriangleup))/(2*a)`

`x_(2) = (-b - √(\bigtriangleup))/(2*a)`

`\bigtriangleup = b^(2) - 4ac`

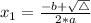
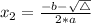
In this question:

`f(t) = -16t^(2) + 320t - 256`

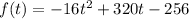
So

`a = -16, b = 320, c = -256`

`\bigtriangleup = (320)^(2) - 4*(-16)*(-256) = 86016`

`t_(1) = (-320 + √(86016))/(2*(-16)) = 0.8348`

`t_(2) = (-320 - √(86016))/(2*(-16)) = 19.17`

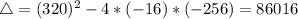
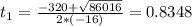
Subtracting:

19.17 - 0.8348 = 18.34

The piano was in the air for 18.34 seconds.