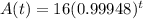Answer:
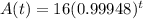
Explanation:
The exponential function is modeled using the equation:
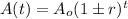
Where the plus sign indicates growth and the negative sign indicates exponential decay.
- r=Decay/Growth constant
- t=time
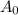 is the starting value.
is the starting value.
For an exponential function has a starting value of 16 and a decay rate of 0.52%.
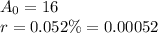
This gives:
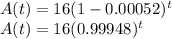
The function that models this situation is: