Answer:
Proved (See Explanation)
Explanation:
Show that 3ⁿ⁺⁴ - 3ⁿ is divisible by 16.
This is done as follows
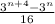
From laws of indices;
aᵐ⁺ⁿ = aᵐ * aⁿ.
So, 3ⁿ⁺⁴ can be written as 3ⁿ * 3⁴.
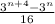 becomes
becomes
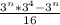
Factorize
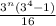

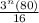
3ⁿ * 5
5(3ⁿ)
The expression can not be further simplified.
However, we can conclude that when 3ⁿ⁺⁴ - 3ⁿ is divisible by 16, because 5(3ⁿ) is a natural whole number as long as n is a natural whole number.